LR 1: Mean Value Theorem

This post begins a multi-part build up to proving L’Hôpital’s rule. In order to build ground up, however, some theorems must be understood, so I’m going to start off with understanding the mean value theorem.

One last thing: the mean value theorem is not really a part of understanding L’Hôpital’s rule, but Cauchy’s mean value theorem is. As Cauchy’s is an extension and generalization of the mean value theorem, I think that it’s important that readers have a good idea of what it is.

THE CONCEPT (finally)

As you’re driving through a highway with a speed limit of 75 mph, you notice that cops are logging cars’ speeds (because they have nothing better to do, I guess). Let’s call this checkpoint A. 20 miles and 15 minutes later, you notice another cop car, but this time, the cops are pulling you over for speeding. You are puzzled because you specifically remember going at 65 mph when they pulled you over. It is later revealed to you that they knew you sped at some point from checkpoint A to wherever you are right now. How do they know that? No, it’s not some fancy tech, but simply the mean value theorem.

Of course, this wouldn’t actually happen because cops have better things to do than do the job of a speed gun, but the deduction is completely possible. By the end of this post, my hope is that you’ll be able to understand how.

In textbook terms, the mean value theorem states that if a function is continuous on and differentiable on , then there must exist a point such that .

Consider the graph of . *

Produced using graphing software, Desmos

NOTE: At this point, I highly recommend checking the applet out and following along (link in footnotes). I’ll also be explaining with images here, but I just think the applet is more intuitive.

Now, let’s add a secant line through it, restricting it to a ≤ x ≤ b, where a and b are values in the domain of the function and a ≤ b

Produced using graphing software, Desmos

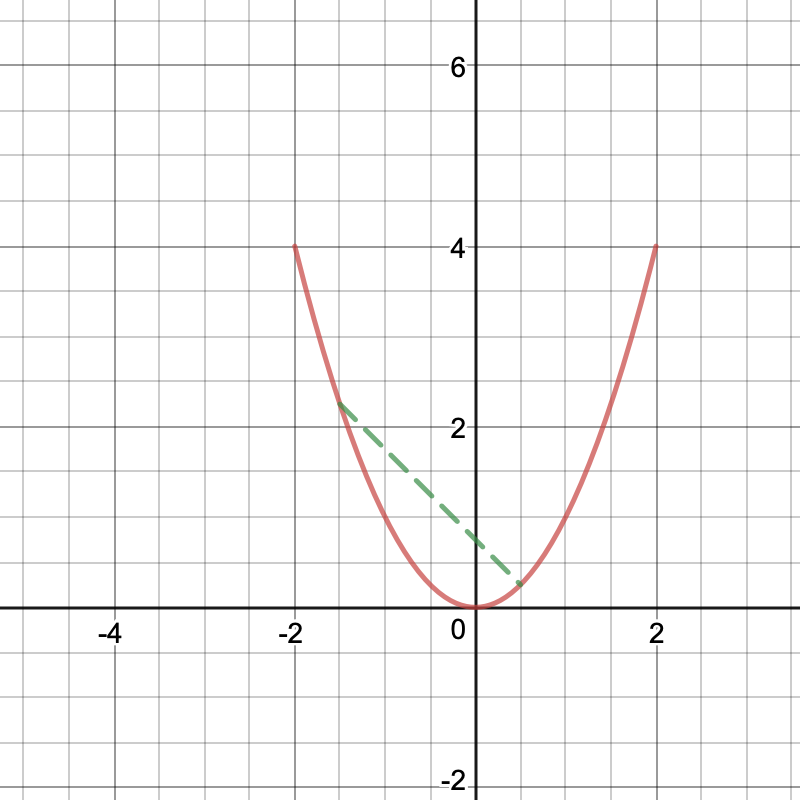
The mean value theorem states that there must be a point on the graph where the tangent is parallel to the secant line. For this secant line, it’s $latex (-0.5, 0.25). However, there’d be a different point for every secant line of the graph.

WHY DOES IT WORK?**

In order to understand why the mean value theorem makes sense, we need to understand tangents.

The slope of a tangent at a point is determined by the derivative of the graph at that point. The derivative of a function is determined by the following expression:

, where h is the change in

Let . If we take the limit part out, the rest of the expression is simply . If this looks familiar, it’s because that expression is the same as the formula for the slope of a line; in this case, it gives you the slope of the secant.

Now, put the limit back in. Essentially, the expression, , finds the slope of the secant when .

Thus, every tangent is developed from a secant, and every secant forms a tangent. Hence, for every secant, there must be a tangent that is parallel.

Now, tie it back to the original question: how did the cops know?

REAL LIFE APPLICATION

Your positions throughout the trip can be described through a function. Your average velocity from A to where you get caught (slope of secant that crosses the function) was 80 miles per hour. The slope of a tangent of the function would be your instantaneous velocity. Thus, by the mean value theorem, at one point, be it a second or an instant, you were going at 80 miles per hour.

Logically, this makes sense. The mean of set values is the value that is right in the middle of the set, i.e. . Thus, if your average was 80, you must have values greater than or equal to 80 in the set.

* use this link if you want to explore it yourself. I couldn’t embed an iframe because WordPress doesn’t allow users on the free version to do so, and I’m broke…

**I’m not going to go over the textbook proof. You can go on Wikipedia for that.