Explaining Derivatives

June 25, 2019

Purpose

Some people told me that I should explain derivatives in my Mean Value Theorem post if I wanted it to be accessible to younger readers. Because that post was already long, I decided to make a separate post for it. This took a while because I wanted to find an intuitive explanation for derivatives, but the most I could come up with was explaining the limit definition, which is basically every high school classroom’s way of explaining it. I finally got an explanation while discussing uniform motion with my cousin. Well, here it is. Enjoy!

Building up the Idea

Planets don’t travel in straight lines: because of the gravity exerted by other celestial bodies, planets’ directions and speeds are altered. But an elliptical orbit means that the rate at which a planet’s position changes is different for different points in the orbit. If you were to run on a circular track, your speed on the straight area would be significantly greater than your speed on the turn.

Back to our planet: basically, its rate of displacement, or velocity, changes. We know the velocity is speed with directional measures, and we know that the speed at which something changes is it slope. Consequently, if a planet’s orbit were to be graphed, its slope would be changing at various points. So how do we find its velocity or slope at a given point, say $(x_1, y_1)$ ?

Produced using the graphing software Desmos

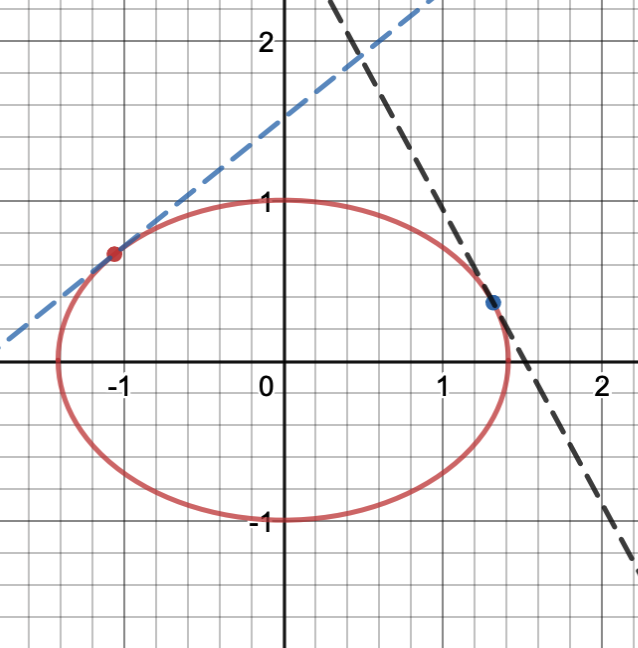
What if every other celestial body but our planet disappeared at $(x_1, y_1)$ ? In other words, what if all external forces were to be eliminated? Well, Newton’s First Law states that an object at rest stays at rest and an object in motion stays in motion at constant velocity. As are result, if every external force was eliminated at $(x_1, y_1)$ , then the planet would continue traveling in the same velocity as it had been at the point. In other words, it would travel on a line that is tangent to the original orbit at $(x_1, y_1)$ . Conversely, the slope of the tangent would be the slope of the orbit at that point.

This brings us to the idea of derivatives, which is often defined as the rate of change at a single point. The problem with this definition, however, is it raises the paradox: change occurs over multiple points. Instantaneous change isn’t possible. Alternatively, derivatives can be defined as the slope of the tangent, a line that touches the function only once, at that point.

Limit Definition

This explanation is probably more intuitive for those with some limits under their belt, but it is a much more abstract idea. Let’s look at what differentiation basically is: Britannica calls it the process of finding the rate of change of a function. In other words, it’s how fast a function changes. If that sounds familiar, it’s because that’s essentially what a slope is. We established in the last section that the slope of the tangent of a function at a certain point IS the slope of the function at that point.

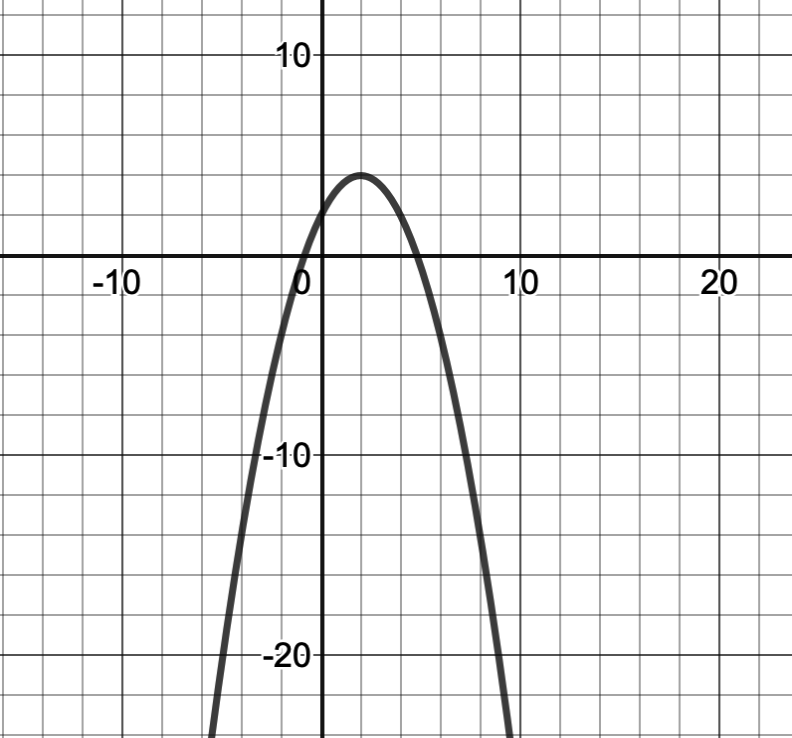
Consider this parabola:

Now let’s add a secant line through it:

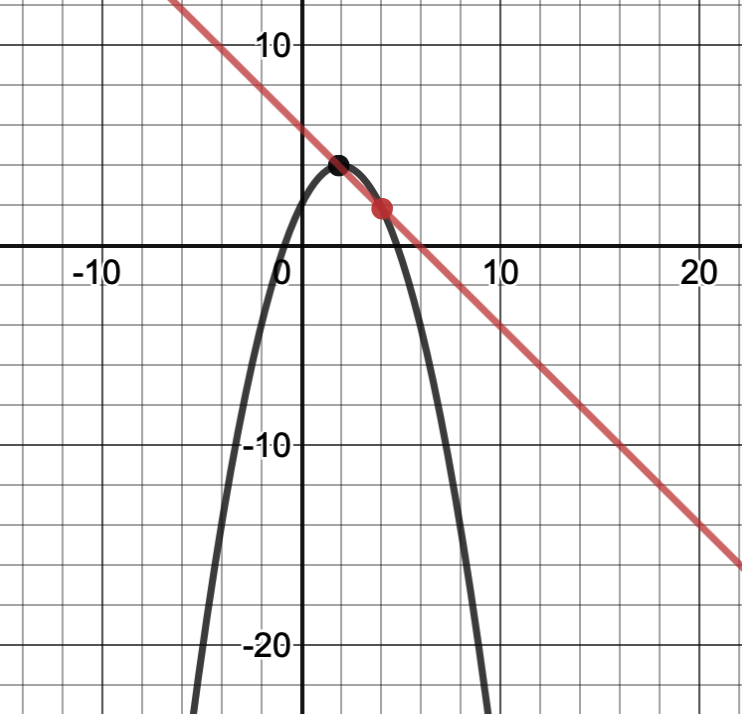
If the red point is at $(x_1, f(x_1) )$ and the black point is at $(x_2, f(x_2) )$ , then the slope of the line would be $\frac {f(x_2) - f(x_1)}{x_2 - x_1}$ . If you think about it, then the value of $x_2 - x_1$ is essentially some $\Delta x$ *. Well, if the last statement is true, then $x_2=x_1 + \Delta x$ . Then, our slope equation becomes $\frac {f(x_1 + \Delta x) - f(x_1)}{(x_1 + \Delta x) - x_1}$ . Because we only have one $x$ , let’s set $x_1 = x$ to reduce bulk. So we have this equation for slope of the secant: $\frac {f(x + \Delta x) - f(x)}{(x + \Delta x) - x}$ . In order to find the slope of the function at, say, the black point, we need to find the slope of the tangent.

In order to find the slope of the function at, say, the black point, we need to find the slope of the tangent at that point. A tangent only touches the function at one point, so the red point and the black point would have to be the same.

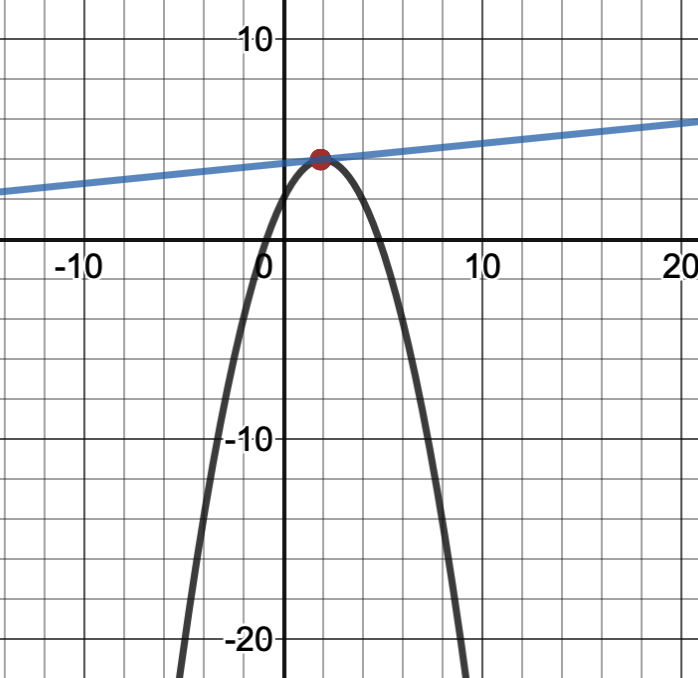
If that’s true, then $x_2 - x_1=0$ . Because $x_2 - x_1=\Delta x$ is also true, by the transitive property, $\Delta x = 0$ . So, we try to solve: $\frac {f(x + 0) - f(x)}{0}$ . Basic arithmetic tells you that this value is indeterminate and that this expression would not make sense. That’s because it doesn’t. Change happens over multiple points; instantaneous change isn’t possible by the very definition of change. So what are we solving for? Well, if we can get values for $\Delta x$ as close to 0 as possible, then we might be able to approximate the value by following the pattern. So essentially, we’ll be solving for this: $\lim_{\Delta x\rightarrow 0} \frac {f(x + \Delta x) - f(x)}{\Delta x}$ . And that, my dear readers, is the limit definition of a derivative.

* $\Delta$ is the symbol for ‘difference’.

2 responses to “Explaining Derivatives”

Blog post explaining derivatives – Nevin Manimala's Blog

June 25, 2019 at 5:59 pm

[…] I’ve been trying to explain fairly complex (high school-calc I or II) concepts in more intuitive sense in my blog https://catoutofbox.wordpress.com . My recent post is on derivatives, which I’ve come to realize is a hard concept to really understand. I would really appreciate some feedback on it and how intuitive the explanation is. If you’re willing to take the time, here’s a link: https://catoutofbox.wordpress.com/2019/06/25/explaining-derivatives/. […]

LikeLike

Reply
Why Integrals? – Cat's Out of Box

November 28, 2019 at 9:06 pm

[…] looked at how limits explain derivatives in an unambiguous and somewhat elegant manner. Unsurprisingly, limits seems to be the foundation […]

LikeLike

Reply

Get updates

From art exploration to the latest archeological findings, all here in our weekly newsletter.