Why Integrals?

We’ve looked at how limits explain derivatives in an unambiguous and somewhat elegant manner. Unsurprisingly, limits seems to be the foundation for integrals as well. It might, however, be a longer pathway, not just because of the proof but also because of the definition of the integral.

Defining the Integral

I find that the definition of the integral (textbook or intuitive) is much more elusive than that of the derivative. After scouring the internet, I was only slightly satisfied with Wolfram Alpha’s definition: a mathematical object that can be interpreted as an area or a generalization of area. That too is convoluted at best. Defining the purpose of definite integration is easy: to find the area underneath a curve. How does the integral get us there?

For now, we might just have to turn to the historical roots of the integral, or this thing:

It looks complicated, almost elusive to the layman, but Gottfried Leibniz simply used it to mean “summation”–if you look at it with Leibniz’s intention in mind, you’d see that it’s simply an elongated “S” (for summation).

Okay, so you may be wondering how is different from . Why use integral calculus when you could use second grade math? The most convincing explanation I found was in The Joy of x, by Steven Strogatz. The things we use integration for tend to change. None of those additives are actual points on a number line. Take, for example, the overall distance traveled by an accelerating car.

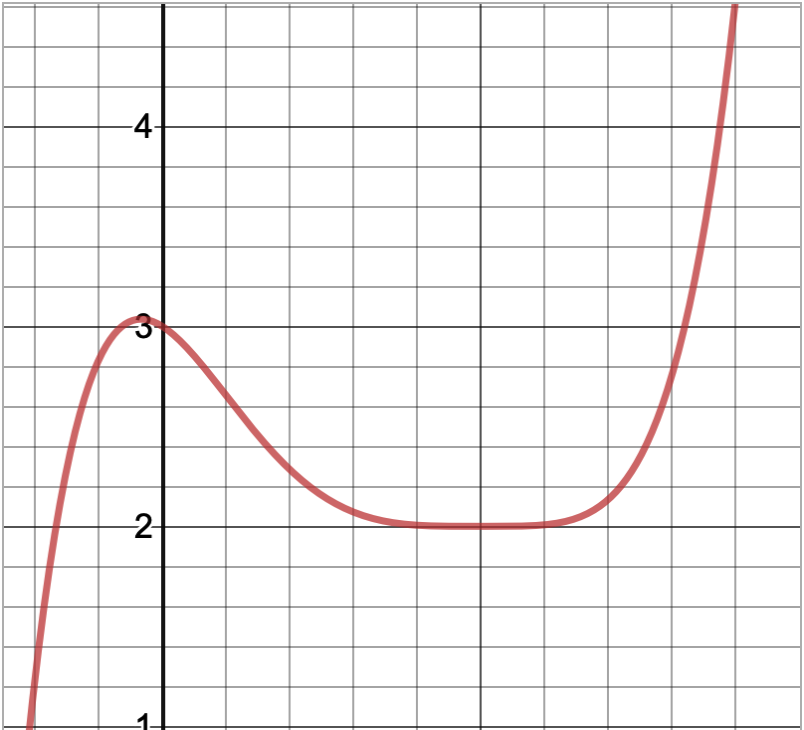
Because distance travelled is impossible to calculate at an instant, there’s no way to simply add up the distance travelled at every single point.

Before we try to figure out a way to find the distance travelled by a car of changing velocity, let’s look at a car that travels at the same velocity:

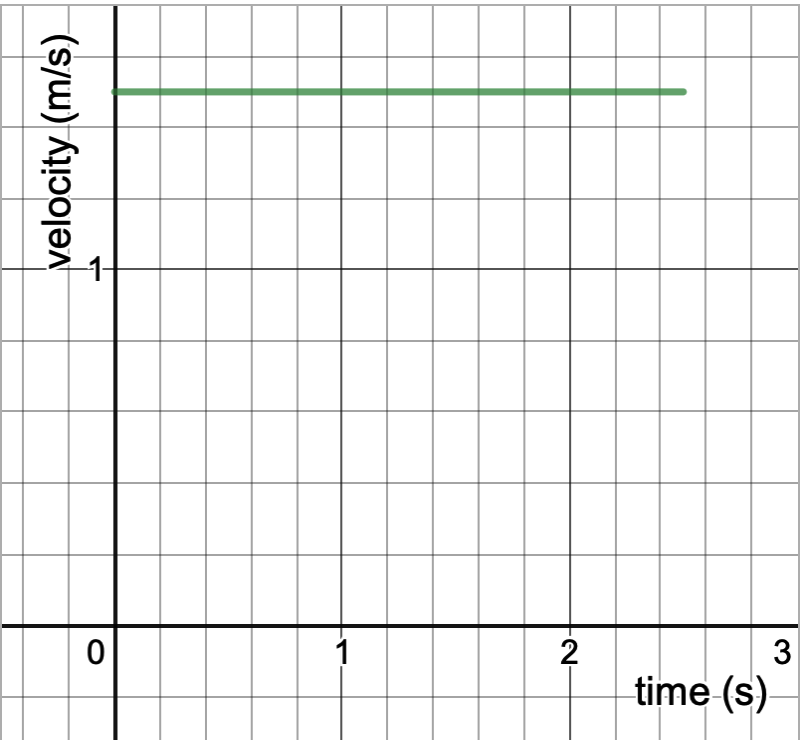
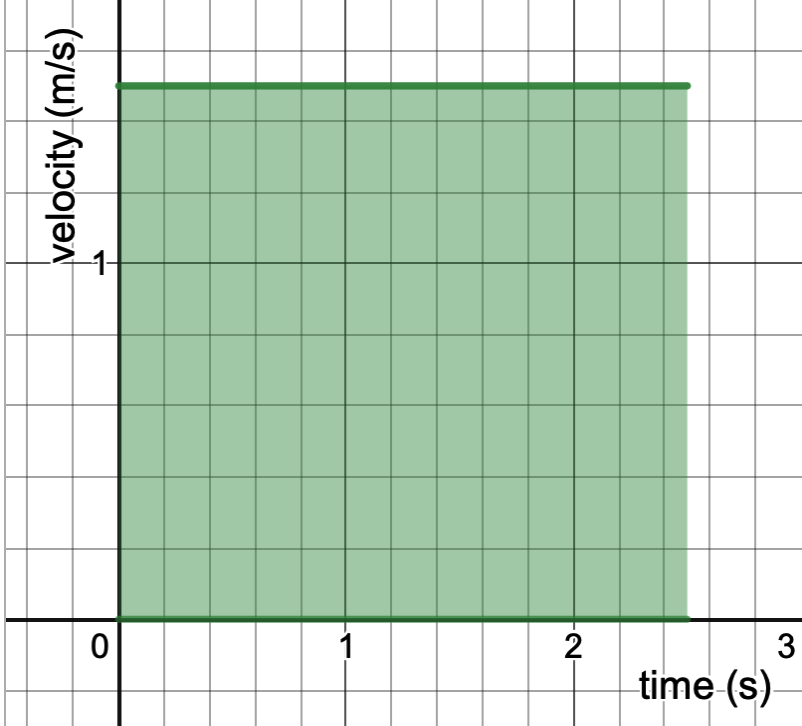
In order to find the distance travelled by a car traveling at 1.5 meters per second for 2.5 seconds, we would simply multiply the velocity by time. You may notice that this is simply the area of a rectangle of side lengths 1.5 and 2.5. Looking at the graph, it’s easy to see that this is simply the area under the graph of .

So what about this car?

Applying the same logic, you’ll have to find the area underneath the curve. Obviously, it’s not as easy as finding the area of a rectangle.

Now, you may have thought of a way around the problem: find the distance travelled at two different intervals, and then average them.

Now, you’re looking at a graph like this:

So the total area would be where is the first interval and is the second.

While this may give you an approximation, it won’t be very accurate. You can see the large area disparity created. What if, instead, we increased the intervals, thus making them shorter?

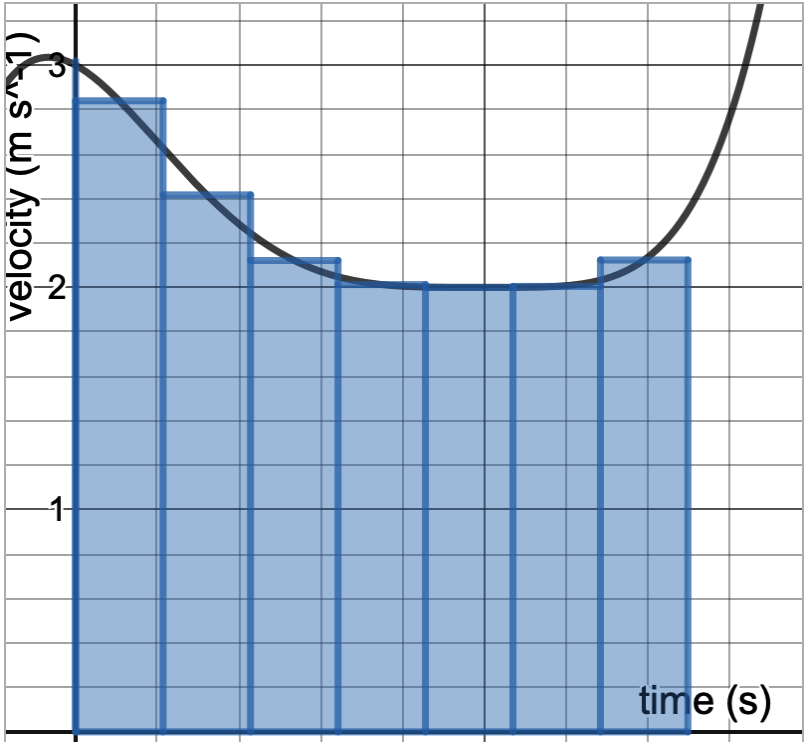
Just by eye-balling, you can see that the difference is much smaller. Now, what if we made the number of rectangles, that is intervals, infinite? Essentially, ? Because these values are no longer physical points on a number line, you’d find it impossible to actually add them up. That essentially is where the idea of integrals come in. An integral is basically .